문제 출처 및 한국정보올림피아드 1차 대회 공식 홈페이지 링크 : https://koi.or.kr/koi/2019/1/
2022년도 한국정보올림피아드 1차 대회
대회 응시자를 위해 공지되었던 안내사항은 응시자 안내사항 페이지에서 확인해 주세요.
koi.or.kr
[유형1] 1번

2019*2021 = 4080399, 2로 계속 나누면 2040199 1020099 510049 255024 127512 ... 이고 이때 나타난 나머지 중 오른쪽부터 연속된 1의 개수는 4개.
[유형1] 2번

3부터 15까지 모두 더하면 117. 117-x = 106, x = 11
[유형1] 3번

16*(20^1) = 320. 13*(20^0) = 13*1= 13. 320+13 = 333
[유형1] 4번

어린이 2명이 건너고, 어린이 한 명이 돌아온 후 어른 한 명이 강을 건넌다. 다시 강의 반대편에 있던 어린이 한 명이 돌아오는 이 4번의 과정을 수행하면 어른 한 명이 건널 수 있다. 20명의 어른이 다 이 4번의 과정을 수행하면 20*4 = 80, 80번 건너면 된다.
[유형1] 5번

일년이일 년이 365일인 연도의 수는 303개, 일 년이 366일인 연도의 수는 97개 이다. 이를 활용해 며칠이 지났는지 확인하면 365*303 = 110595, 366*97 = 35502, 110595+35502 = 145797, 145797일이 지났다. 일주일은 7일임으로 7로 나누면 20871로 나머지 없이 나누어 떨어진다. 이는 월요일에서 0일이 지난, 월요일이라는 뜻이다.
[유형1] 6번

한붓그리기의 법칙 (연결되어 있는 점들의 수가 홀수개인 점들이 0개이거나 2개인 도형만 한붓그리기 가능) 에 따라 3개가 제외된다. 나머지 2개만 살펴보면 아래 모양이 두붓그리기가 가능하다.

[유형1] 7번

위상정렬 문제이다. 꼭 위상정렬을 쓰지 않고 2명이 가능한 일들을 지우면서 시간을 계산해 보면 7시간이다.

[유형1] 8번

규칙 3을 이용하여 7개의 원판을 2개씩 묶어 원판 4개로 생각한다. (2개짜리 원판 3개, 1개짜리 원판 1개) 원판 4개를 옮기기 위해 필요한 횟수는 15번이다. (A[n] = 2*A[n-1]+1)
[유형1] 9번

회문이어서 5번째 자리까지만 생각한다. aaaaa는 첫 번째일것이고, baaaa는 82번째, caaaa는 163번째이다. 200에 가장 근접한 수인 163으로 인해 첫번째 자리는 c이다. caaaa는 163, cbaaa는 190, ccaaa는 217로 200보다 작고 가장 근접한 수인 190으로 인해 두 번째 자리는 b이다. cbaaa는 190, cbbaa는 199번째, cbcaa는 208로 세 번째 자리는 b이다. cbbaa는 199, cbbba는 202, cbbca는 205로 네 번째는 a, cbbaa는 199, cbbab는 200, cbbac는 201로 다섯 번째 자리는 b이다. 이 다섯 자리로 회문을 만들면 cbbababbc이다. (9글자 회문이어서 5번째 상관 안 씀)
[유형1] 10번

길이를 1이라 생각하면 1개의 방법으로 넣을 수 있고, 2라 생각하면 2개, 3이라 생각하면 3개, 4라 생각하면 5개의 방법, 5라 생각하면 8개의 방법으로 넣을 수 있다. 이를 통해 길이를 N이라 한다면 f[N] = f[N-1]+f[N-2] 라는 것을 알 수 있다. 그럼 13, 21, 34, 55, 89의 순으로 늘어나고 N이 10일 때는 89이다.
[유형1] 11번

쌍을 구해보면 3-4, 3-5, 3-6, 4-5, 4-6, 5-6 이 있다. 3-4의 쌍은 3, 7, 10, 11, 13, 14... 개의 성냥으로 만들 수 있고 13개 이상의 성냥으로는 모두 만들 수 있다. 3-5의 쌍에서는 8, 11, 13, 14, 16, 17...로 16 이상에서, 4-5에서는 9, 13, 14, 17, 18, 19, 21, 22... 로 21 이상에서, 5-6의 쌍에서는 11, 16, 17, 21, 22, 23, 26, 27, 28, 29, 31, 32... 로 31 이상의 수에서는 모두 구할 수 있다.
아직 구하지 않은 3-6의 쌍을 보면 9, 12, 15, 18, 21, 24로 3의 배수에서만 만들 수 있고 4-6의 쌍에서는 10, 14, 16, 18, 20... 으로 2의 배수에서만 만들 수 있다. 이를 통해 모든 조건을 정리해 보면 2의 배수, 그리고 3의 배수 이면서 31 이상의 수 즉 31 이상의 수 중 6의 배수 중 가장 작은 수를 구하면 된다. 답은 36이다.
[유형1] 12번
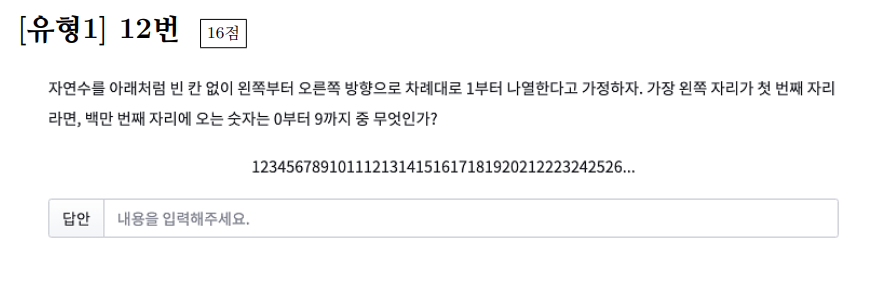
일의 자리에서는 1부터 9까지의 수가 있고, 총 9자리를 차지한다. 십의 자리에서는 10부터 99까지의 90개의 수가 있고 각 2자리씩 차지하기 때문에 총 180자리를 차지한다. 이런 식으로 쭉 계산한다면 백의 자리에서는 100부터 999까지 2700의 자리를 차지하고, 천의 자리에서는 1000부터 9999까지 36000의 자리를, 만의 자리에서는 10000부터 99999까지 450000 자리를, 십만의 자리에서는 100000부터 999999까지 5400000의 자리를 차지한다. 일의 자리에서 만의 자리까지 차지하는 자릿수의 합을 모두 더하면 488889이고, 이를 백만 자리의 수에서 빼면 511111, 99999부터 511111의 자리를 더 채워야 한다. 뒤 십만의 자리는 한 수당 6자리를 차지하므로 남은 자릿수인 511111을 6으로 나누면 85185...1로 99999부터 85185만큼의 수가 더 생긴 후 첫 번째 칸이다. 185185의 첫번째 수인 1이 답이다.
저도 중등부 대회 나갔던 사람으로 풀이가 확실하게 맞지 않을 수 있습니다!
피드백, 지적, 질문 편하게 해 주세요 :)
'🏅 대회 > 한국정보올림피아드 (KOI)' 카테고리의 다른 글
| 2023 정보올림피아드 중등부 1차 후기 (0) | 2023.05.28 |
|---|---|
| 2020 KOI(한국정보올림피아드) 중등부 1차 1교시 문제풀이 (1번~12번) (0) | 2023.04.23 |
| 2022 KOI(한국정보올림피아드) 중등부 1차 1교시 문제풀이 (13번~20번) (0) | 2023.02.26 |
| 2021 KOI(한국정보올림피아드) 중등부 1차 1교시 문제 풀이 (1번~12번) (4) | 2023.01.23 |
| 2022 KOI(한국정보올림피아드) 중등부 1차 1교시 문제 풀이 (7번~11번) (3) | 2022.12.04 |


